| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Section A | Section B | Section C | Section D |
Class 10th Mathematics Sample Paper Set II (NCERT Exemplar)
Welcome to a vital collection of Class 10 Mathematics Sample Papers, accompanied by their exceptionally detailed solutions. These papers are meticulously crafted not just as practice exercises, but as comprehensive assessment tools designed to offer students a truly realistic examination experience. They intentionally mirror the challenging nature, diverse question formats, and syllabus weightage characteristic of final examinations, particularly emphasizing the application-oriented and concept-testing style synonymous with the respected NCERT Exemplar series. The goal is to thoroughly evaluate understanding beyond rote memorization, focusing on problem-solving abilities and higher-order thinking skills (HOTS).
Each sample paper within this collection comes with an exhaustive solutions set, providing complete, step-by-step answers and clear explanations for every single question. This comprehensive support covers the full spectrum of question types you are likely to encounter:
- Multiple Choice Questions (MCQs)
- Fill-in-the-Blanks
- True/False Statements
- Very Short Answer (VSA) Questions
- Short Answer (SA) Questions
- Long Answer (LA) Questions
The questions themselves are drawn from across the entire Class 10 Mathematics syllabus, ensuring a well-rounded assessment. The solutions demonstrate the necessary techniques, calculations, proofs, and logical reasoning required for topics spanning Real Numbers, Polynomials, Pairs of Linear Equations, Quadratic Equations (including the discriminant $D = b^2 - 4ac$ and the quadratic formula $x = \frac{-b \pm \sqrt{D}}{2a}$), Arithmetic Progressions (using $a_n = a+(n-1)d$ and $S_n = \frac{n}{2}[2a+(n-1)d]$), Triangles (covering similarity criteria and the Pythagoras theorem), Coordinate Geometry, Introduction to Trigonometry and its Applications (including identities like $\sin^2\theta + \cos^2\theta = 1$ and height/distance problems), Circles (focusing on tangents), Constructions (with justifications), Areas Related to Circles (sectors, segments like Area = $\frac{\theta}{360}\pi r^2$), Surface Areas & Volumes (combinations, conversions, frustum, e.g., Volume of Sphere = $\frac{4}{3}\pi r^3$), Statistics (Mean, Median, Mode for grouped data), and Probability (calculating theoretical probability $P(E) = \frac{n(E)}{n(S)}$).
The provided solutions strive to emulate the standard expected in board examinations that incorporate HOTS questions, focusing on demonstrating the complete working process, not just the final result. This includes showing the application of relevant formulas, detailing algebraic manipulations, providing rigorous justifications for geometric proofs, outlining construction steps precisely, plotting graphs accurately where needed, and offering clear, concise explanations. A key feature is illustrating how concepts from seemingly disparate chapters can be integrated within a single, multi-faceted problem – a hallmark of the Exemplar standard.
By diligently working through these solved sample papers, students can effectively gauge their overall preparedness, gain familiarity with examination patterns and potential marking schemes, practice crucial time management skills under simulated conditions, identify specific areas of weakness across different chapters when faced with mixed problems, learn effective strategies for presenting answers clearly and logically, and become accustomed to the type and difficulty level of questions that require deep conceptual understanding and application. These solved papers serve as indispensable final-stage preparation tools, crucial for building confidence and achieving comprehensive readiness for Class 10 Mathematics examinations.
Section A
Question 1. The largest number which divides 318 and 739 leaving remainders 3 and 4, respectively is
(A) 110
(B) 7
(C) 35
(D) 105
Answer:
Solution
Let the required largest number be $N$.
According to the problem, when 318 is divided by $N$, the remainder is 3. This implies that $318 - 3$ must be exactly divisible by $N$.
Similarly, when 739 is divided by $N$, the remainder is 4. This implies that $739 - 4$ must be exactly divisible by $N$.
We calculate the values that are exactly divisible by $N$:
$318 - 3 = 315$
$739 - 4 = 735$
The number $N$ must be a common divisor of 315 and 735. Since we are looking for the largest such number, $N$ is the Greatest Common Divisor (GCD) of 315 and 735.
We find the prime factorization of 315 and 735 to determine their GCD.
Prime factorization of 315:
$\begin{array}{c|cc} 3 & 315 \\ \hline 3 & 105 \\ \hline 5 & 35 \\ \hline 7 & 7 \\ \hline & 1 \end{array}$
So, the prime factorization of 315 is $3^2 \times 5^1 \times 7^1$.
Prime factorization of 735:
$\begin{array}{c|cc} 3 & 735 \\ \hline 5 & 245 \\ \hline 7 & 49 \\ \hline 7 & 7 \\ \hline & 1 \end{array}$
So, the prime factorization of 735 is $3^1 \times 5^1 \times 7^2$.
The GCD of two numbers is found by taking the product of the common prime factors, each raised to the lowest power that appears in the factorizations:
The common prime factors are 3, 5, and 7.
Lowest power of 3 is $3^1$.
Lowest power of 5 is $5^1$.
Lowest power of 7 is $7^1$.
GCD$(315, 735) = 3^1 \times 5^1 \times 7^1$
GCD$(315, 735) = 3 \times 5 \times 7$
$3 \times 5 \times 7 = 15 \times 7 = 105$
Thus, the largest number that divides 318 and 739 leaving remainders 3 and 4, respectively, is 105.
This corresponds to option (D).
The final answer is 105.
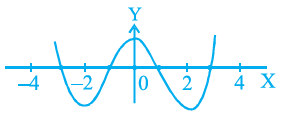
Question 2. The number of zeroes lying between –2 to 2 of the polynomial f (x), whose graph is given below, is
(A) 2
(B) 3
(C) 4
(D) 1
Answer:
Solution
The zeroes of a polynomial $f(x)$ are the values of $x$ for which $f(x) = 0$. Graphically, these are the points where the graph of $y = f(x)$ intersects or touches the x-axis.
The question asks for the number of zeroes lying between –2 and 2. This means we need to count the number of times the graph intersects the x-axis for $x$ values strictly greater than –2 and strictly less than 2.
We need to observe the graph provided and count the number of intersections with the x-axis within the interval $(-2, 2)$.
Looking at the graph:
1. The graph intersects the x-axis at approximately $x = -1.5$. This value is between –2 and 2.
2. The graph intersects the x-axis at $x = 0$. This value is between –2 and 2.
3. The graph intersects the x-axis at approximately $x = 1.5$. This value is between –2 and 2.
4. The graph intersects the x-axis at approximately $x = 2.5$. This value is not between –2 and 2 (as it is greater than 2).
Therefore, there are 3 points where the graph intersects the x-axis for $x$ values between –2 and 2.
The number of zeroes lying between –2 to 2 is 3.
This corresponds to option (B).
The number of zeroes between –2 and 2 is 3.
Question 3. The discriminant of the quadratic equation 3$\sqrt{3}$ x2 + 10x + $\sqrt{3}$ = 0 is
(A) 8
(B) 64
(C) $-\frac{1}{3\sqrt{3}}$
(D) $-\sqrt{3}$
Answer:
Solution
The given quadratic equation is $3\sqrt{3}x^2 + 10x + \sqrt{3} = 0$.
This equation is in the standard form of a quadratic equation, $ax^2 + bx + c = 0$, where:
$a = 3\sqrt{3}$
$b = 10$
$c = \sqrt{3}$
The discriminant of a quadratic equation $ax^2 + bx + c = 0$ is given by the formula $D = b^2 - 4ac$.
Substitute the values of $a$, $b$, and $c$ into the discriminant formula:
$D = (10)^2 - 4 \times (3\sqrt{3}) \times (\sqrt{3})$
$D = 100 - 4 \times 3 \times (\sqrt{3} \times \sqrt{3})$
We know that $\sqrt{3} \times \sqrt{3} = (\sqrt{3})^2 = 3$.
$D = 100 - 4 \times 3 \times 3$
$D = 100 - 12 \times 3$
$D = 100 - 36$
$D = 64$
The discriminant of the given quadratic equation is 64.
This value corresponds to option (B).
The discriminant is 64.
Question 4. If $\frac{6}{5}$ , a , 4 are in AP, the value of a is
(A) 1
(B) 13
(C) $\frac{13}{5}$
(D) $\frac{26}{5}$
Answer:
Solution
Given that the three terms $\frac{6}{5}$, $a$, and 4 are in Arithmetic Progression (AP).
In an AP, the difference between consecutive terms is constant. This common difference is the same throughout the sequence.
Let the three terms be $t_1 = \frac{6}{5}$, $t_2 = a$, and $t_3 = 4$.
The condition for these terms to be in AP is that the difference between the second term and the first term is equal to the difference between the third term and the second term.
$t_2 - t_1 = t_3 - t_2$
Substitute the given terms into this equation:
$a - \frac{6}{5} = 4 - a$
Now, we solve this linear equation for $a$.
Add $a$ to both sides of the equation:
$a + a - \frac{6}{5} = 4 - a + a$
$2a - \frac{6}{5} = 4$
Add $\frac{6}{5}$ to both sides of the equation:
$2a - \frac{6}{5} + \frac{6}{5} = 4 + \frac{6}{5}$
$2a = 4 + \frac{6}{5}$
To add the numbers on the right side, find a common denominator:
$2a = \frac{4 \times 5}{5} + \frac{6}{5}$
$2a = \frac{20}{5} + \frac{6}{5}$
$2a = \frac{20 + 6}{5}$
$2a = \frac{26}{5}$
Divide both sides by 2 to isolate $a$:
$a = \frac{26}{5 \times 2}$
$a = \frac{26}{10}$
Simplify the fraction by cancelling the common factor of 2:
$a = \frac{\cancel{26}^{13}}{\cancel{10}_{5}}$
$a = \frac{13}{5}$
Alternatively, the middle term of three terms in an AP is the arithmetic mean of the first and third terms.
$a = \frac{\text{first term} + \text{third term}}{2}$
$a = \frac{\frac{6}{5} + 4}{2}$
Calculate the sum in the numerator:
$\frac{6}{5} + 4 = \frac{6}{5} + \frac{4 \times 5}{5} = \frac{6}{5} + \frac{20}{5} = \frac{6 + 20}{5} = \frac{26}{5}$
Substitute this sum back into the equation for $a$:
$a = \frac{\frac{26}{5}}{2}$
Dividing by 2 is the same as multiplying by $\frac{1}{2}$:
$a = \frac{26}{5} \times \frac{1}{2}$
$a = \frac{26 \times 1}{5 \times 2}$
$a = \frac{26}{10}$
Simplify the fraction:
$a = \frac{\cancel{26}^{13}}{\cancel{10}_{5}}$
$a = \frac{13}{5}$
The value of $a$ is $\frac{13}{5}$. This matches option (C).
The value of $a$ is $\frac{13}{5}$.
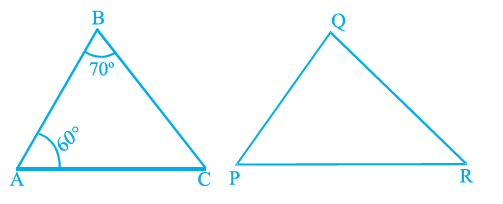
Question 5. If in the following figure, ∆ ABC ~ ∆ QPR, then the measure of ∠Q is
(A) 60°
(B) 90°
(C) 70°
(D) 50°
Answer:
Solution
Given that $\triangle ABC$ is similar to $\triangle QPR$, which is written as $\triangle ABC \sim \triangle QPR$.
From the figure, we have the angles of $\triangle ABC$:
$\angle A = 50^\circ$
$\angle B = 60^\circ$
When two triangles are similar, their corresponding angles are equal. The similarity statement $\triangle ABC \sim \triangle QPR$ tells us the correspondence between the vertices and hence the angles.
The correspondence is as follows:
Vertex A corresponds to Vertex Q
Vertex B corresponds to Vertex P
Vertex C corresponds to Vertex R
Therefore, the corresponding angles are equal:
$\angle A = \angle Q$
$\angle B = \angle P$
$\angle C = \angle R$
We are asked to find the measure of $\angle Q$. From the angle correspondence, we know that $\angle Q = \angle A$.
From the figure, we are given that $\angle A = 50^\circ$.
Substituting the value of $\angle A$, we get:
$\angle Q = 50^\circ$
We can also find the third angle in $\triangle ABC$ using the angle sum property of a triangle:
$\angle A + \angle B + \angle C = 180^\circ$
$50^\circ + 60^\circ + \angle C = 180^\circ$
$110^\circ + \angle C = 180^\circ$
$\angle C = 180^\circ - 110^\circ$
$\angle C = 70^\circ$
Based on the similarity $\triangle ABC \sim \triangle QPR$, we would have $\angle P = \angle B = 60^\circ$ and $\angle R = \angle C = 70^\circ$. The figure shows $\angle P = 70^\circ$, which is inconsistent with the stated similarity and the angles of $\triangle ABC$. However, the question asks for $\angle Q$ based on the given similarity statement $\triangle ABC \sim \triangle QPR$ and the angles in the figure. The correspondence $\angle Q = \angle A$ derived from the stated similarity is clear, and $\angle A = 50^\circ$ is given in the figure.
Thus, the measure of $\angle Q$ is $50^\circ$. This matches option (D).
The measure of $\angle Q$ is $50^\circ$.
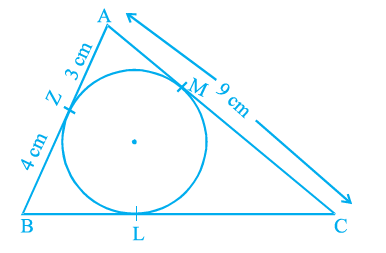
Question 6. In the adjoining figure, ∆ ABC is circumscribing a circle. Then, the length of BC is
(A) 7 cm
(B) 8 cm
(C) 9 cm
(D) 10 cm
Answer:
Solution
When a triangle circumscribes a circle, the lengths of tangents from a vertex to the points of contact are equal.
Let the points of tangency on AB, BC, and AC be D, E, and F respectively.
From the figure, we are given the lengths of segments AD, BD, AF, and CF.
Applying the tangent property:
$AD = AF = 4$ cm
$BD = BE = 3$ cm
$CF = CE$
The side BC is formed by the sum of segments BE and CE.
$BC = BE + CE$
We know $BE = 3$ cm. We need to find CE.
From the figure, the label near C on side BC is 4 cm. Assuming this indicates $CE = 4$ cm (and consequently $CF = 4$ cm by tangent property, despite the label $CF=3$ in the figure being inconsistent), we can find BC.
$BC = BE + CE$
$BC = 3 \text{ cm} \$+\$ 4 \text{ cm}$
$BC = 7$ cm
This result matches option (A).
Note: The figure has an inconsistency as $CF$ is labelled 3 cm, but if $CE=4$, then $CF$ should be 4 cm by the tangent property. Assuming the options and the lengths 3 and 4 on BC are correct, the length of BC is 7 cm.
The length of BC is 7 cm.
Question 7. If sin θ = $\frac{1}{3}$ then the value of (9 cot2 θ + 9) is
(A) 1
(B) 81
(C) 9
(D) $\frac{1}{81}$
Answer:
Given:
$\sin \theta = \frac{1}{3}$
To Find:
The value of $(9 \cot^2 \theta + 9)$.
Solution:
We need to evaluate the expression $9 \cot^2 \theta + 9$.
We can factor out 9 from the expression:
$9 \cot^2 \theta + 9 = 9 (\cot^2 \theta + 1)$
We use the fundamental trigonometric identity:
$\text{cosec}^2 \theta - \cot^2 \theta = 1$
Rearranging this identity, we get:
$\cot^2 \theta + 1 = \text{cosec}^2 \theta$
Substitute this into the expression:
$9 (\cot^2 \theta + 1) = 9 \text{ cosec}^2 \theta$
We know that $\text{cosec} \theta$ is the reciprocal of $\sin \theta$.
$\text{cosec} \theta = \frac{1}{\sin \theta}$
Given $\sin \theta = \frac{1}{3}$, we find $\text{cosec} \theta$:
$\text{cosec} \theta = \frac{1}{1/3} = 3$
Now, we calculate $\text{cosec}^2 \theta$:
$\text{cosec}^2 \theta = (3)^2 = 9$
Substitute the value of $\text{cosec}^2 \theta$ back into the expression $9 \text{ cosec}^2 \theta$:
$9 \times 9 = 81$
Alternate Solution:
Given $\sin \theta = \frac{1}{3}$. We can construct a right-angled triangle where the angle is $\theta$.
Let the opposite side to angle $\theta$ be 1 unit and the hypotenuse be 3 units, as $\sin \theta = \frac{\text{Opposite}}{\text{Hypotenuse}}$.
Using the Pythagorean theorem, $a^2 + b^2 = c^2$, where $a$ is the opposite side, $b$ is the adjacent side, and $c$ is the hypotenuse.
$1^2 + (\text{Adjacent})^2 = 3^2$
$1 + (\text{Adjacent})^2 = 9$
$(\text{Adjacent})^2 = 9 - 1 = 8$
Adjacent side $= \sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2}$.
Now we can find $\cot \theta$. $\cot \theta = \frac{\text{Adjacent}}{\text{Opposite}}$.
$\cot \theta = \frac{2\sqrt{2}}{1} = 2\sqrt{2}$
Next, calculate $\cot^2 \theta$:
$\cot^2 \theta = (2\sqrt{2})^2 = 2^2 \times (\sqrt{2})^2 = 4 \times 2 = 8$
Finally, substitute the value of $\cot^2 \theta$ into the given expression:
$9 \cot^2 \theta + 9 = 9 (8) + 9$
$9 \times 8 + 9 = 72 + 9 = 81$
Both methods yield the same result, 81. This corresponds to option (B).
The value of $(9 \cot^2 \theta + 9)$ is 81.
Question 8. The radii of the ends of a frustum of a cone 40 cm high are 20 cm and 11 cm. Its slant height is
(A) 41 cm
(B) 20$\sqrt{5}$ cm
(C) 49 cm
(D) $\sqrt{521}$ cm
Answer:
Given:
Height of the frustum, $h = 40$ cm
Radius of the larger base, $R = 20$ cm
Radius of the smaller base, $r = 11$ cm
To Find:
The slant height, $l$, of the frustum.
Solution:
The formula for the slant height $l$ of a frustum of a cone is given by:
$l = \sqrt{h^2 + (R - r)^2}$
Substitute the given values into the formula:
$l = \sqrt{(40 \text{ cm})^2 + (20 \text{ cm} - 11 \text{ cm})^2}$
$l = \sqrt{(40)^2 + (9)^2}$
Calculate the squares:
$(40)^2 = 1600$
$(9)^2 = 81$
Substitute these values back into the equation for $l$:
$l = \sqrt{1600 + 81}$
$l = \sqrt{1681}$
Now, calculate the square root of 1681.
We can find the square root by checking the options or using calculation.
Consider $41^2 = (40+1)^2 = 40^2 + 2(40)(1) + 1^2 = 1600 + 80 + 1 = 1681$.
So, $\sqrt{1681} = 41$.
$l = 41$ cm
The slant height of the frustum is 41 cm. This matches option (A).
The slant height is 41 cm.
Question 9. A bag contains 40 balls out of which some are red, some are blue and remaining are black. If the probability of drawing a red ball is $\frac{11}{20}$ and that of blue ball is $\frac{1}{5}$ , then the number of black balls is
(A) 5
(B) 25
(C) 10
(D) 30
Answer:
Given:
Total number of balls in the bag = 40
Let $N_{total} = 40$.
The balls are of three colours: red, blue, and black.
Let $N_{red}$ be the number of red balls.
Let $N_{blue}$ be the number of blue balls.
Let $N_{black}$ be the number of black balls.
So, $N_{total} = N_{red} + N_{blue} + N_{black}$.
The probability of drawing a red ball is $P(\text{red}) = \frac{\text{Number of red balls}}{\text{Total number of balls}} = \frac{N_{red}}{N_{total}}$.
Given $P(\text{red}) = \frac{11}{20}$.
So, $\frac{N_{red}}{40} = \frac{11}{20}$.
$N_{red} = \frac{11}{20} \times 40 = 11 \times \frac{\cancel{40}^2}{\cancel{20}_1} = 11 \times 2 = 22$.
Number of red balls, $N_{red} = 22$.
The probability of drawing a blue ball is $P(\text{blue}) = \frac{\text{Number of blue balls}}{\text{Total number of balls}} = \frac{N_{blue}}{N_{total}}$.
Given $P(\text{blue}) = \frac{1}{5}$.
So, $\frac{N_{blue}}{40} = \frac{1}{5}$.
$N_{blue} = \frac{1}{5} \times 40 = \frac{\cancel{40}^8}{\cancel{5}_1} = 8$.
Number of blue balls, $N_{blue} = 8$.
To Find:
The number of black balls, $N_{black}$.
Solution:
We know that the total number of balls is the sum of the number of balls of each colour:
$N_{total} = N_{red} + N_{blue} + N_{black}$
Substitute the known values:
$40 = 22 + 8 + N_{black}$
$40 = 30 + N_{black}$
Subtract 30 from both sides:
$40 - 30 = N_{black}$
$10 = N_{black}$
The number of black balls is 10.
Alternate Solution:
The sum of the probabilities of all possible outcomes is 1.
$P(\text{red}) + P(\text{blue}) + P(\text{black}) = 1$
Given $P(\text{red}) = \frac{11}{20}$ and $P(\text{blue}) = \frac{1}{5}$.
Substitute these values:
$\frac{11}{20} + \frac{1}{5} + P(\text{black}) = 1$
Find a common denominator for the fractions (20):
$\frac{11}{20} + \frac{1 \times 4}{5 \times 4} + P(\text{black}) = 1$
$\frac{11}{20} + \frac{4}{20} + P(\text{black}) = 1$
$\frac{11 + 4}{20} + P(\text{black}) = 1$
$\frac{15}{20} + P(\text{black}) = 1$
Simplify the fraction $\frac{15}{20} = \frac{\cancel{15}^3}{\cancel{20}_4} = \frac{3}{4}$.
$\frac{3}{4} + P(\text{black}) = 1$
Subtract $\frac{3}{4}$ from both sides:
$P(\text{black}) = 1 - \frac{3}{4} = \frac{4}{4} - \frac{3}{4} = \frac{4 - 3}{4} = \frac{1}{4}$.
The probability of drawing a black ball is $\frac{1}{4}$.
The probability of drawing a black ball is also $\frac{\text{Number of black balls}}{\text{Total number of balls}} = \frac{N_{black}}{40}$.
So, $\frac{N_{black}}{40} = \frac{1}{4}$.
Multiply both sides by 40:
$N_{black} = \frac{1}{4} \times 40 = \frac{\cancel{40}^{10}}{\cancel{4}_1} = 10$.
The number of black balls is 10.
Both methods show that the number of black balls is 10. This corresponds to option (C).
The number of black balls is 10.
Question 10. Two coins are tossed simultaneously. The probability of getting at most one head is
(A) $\frac{1}{4}$
(B) $\frac{1}{2}$
(C) $\frac{3}{4}$
(D) 1
Answer:
Solution
When two coins are tossed simultaneously, the possible outcomes are:
Head on the first coin and Head on the second coin (HH)
Head on the first coin and Tail on the second coin (HT)
Tail on the first coin and Head on the second coin (TH)
Tail on the first coin and Tail on the second coin (TT)
The sample space $S$ is the set of all possible outcomes:
$S = \{HH, HT, TH, TT\}$
The total number of possible outcomes is the number of elements in the sample space:
Total number of outcomes = $|S| = 4$
We are interested in the event of getting "at most one head". This means getting either zero heads or exactly one head.
Let $E$ be the event of getting at most one head.
Outcomes with zero heads: TT
Outcomes with exactly one head: HT, TH
The set of favorable outcomes for event $E$ is:
$E = \{TT, HT, TH\}$
The number of favorable outcomes is the number of elements in the set $E$:
Number of favorable outcomes = $|E| = 3$
The probability of an event $E$ is given by the formula:
$P(E) = \frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes}}$
$P(\text{at most one head}) = \frac{|E|}{|S|} = \frac{3}{4}$
The probability of getting at most one head is $\frac{3}{4}$.
This corresponds to option (C).
The probability of getting at most one head is $\frac{3}{4}$.
Section B
Question 11. Which of the following can be the nth term of an AP?
3n + 1, 2n2 + 3, n3 + n.
Give reasons.
Answer:
Solution
An Arithmetic Progression (AP) is a sequence of numbers such that the difference between the consecutive terms is constant. This constant difference is called the common difference, denoted by $d$.
The general form of the $n^{th}$ term of an AP is given by $a_n = a + (n-1)d$, where $a$ is the first term and $d$ is the common difference.
Expanding this formula, we get $a_n = a + nd - d = dn + (a-d)$. This shows that the $n^{th}$ term of an AP is always a linear expression in $n$, i.e., of the form $An + B$, where A and B are constants.
Let's examine each given expression:
Expression 1: $3n + 1$
This expression is of the form $An + B$, where $A = 3$ and $B = 1$. It is a linear expression in $n$.
Let's find the first few terms if $a_n = 3n + 1$:
$a_1 = 3(1) + 1 = 4$
$a_2 = 3(2) + 1 = 7$
$a_3 = 3(3) + 1 = 10$
The sequence is 4, 7, 10, ...
The difference between consecutive terms is $a_2 - a_1 = 7 - 4 = 3$ and $a_3 - a_2 = 10 - 7 = 3$.
Since the difference is constant (3), this sequence is an AP. Thus, $3n + 1$ can be the $n^{th}$ term of an AP.
Expression 2: $2n^2 + 3$
This expression involves $n^2$, so it is a quadratic expression in $n$. It is not in the linear form $An + B$.
Let's find the first few terms if $a_n = 2n^2 + 3$:
$a_1 = 2(1)^2 + 3 = 2(1) + 3 = 5$
$a_2 = 2(2)^2 + 3 = 2(4) + 3 = 8 + 3 = 11$
$a_3 = 2(3)^2 + 3 = 2(9) + 3 = 18 + 3 = 21$
The sequence is 5, 11, 21, ...
The difference between consecutive terms is $a_2 - a_1 = 11 - 5 = 6$ and $a_3 - a_2 = 21 - 11 = 10$.
Since the difference between consecutive terms is not constant ($6 \neq 10$), this sequence is not an AP. Thus, $2n^2 + 3$ cannot be the $n^{th}$ term of an AP.
Expression 3: $n^3 + n$
This expression involves $n^3$, so it is a cubic expression in $n$. It is not in the linear form $An + B$.
Let's find the first few terms if $a_n = n^3 + n$:
$a_1 = 1^3 + 1 = 1 + 1 = 2$
$a_2 = 2^3 + 2 = 8 + 2 = 10$
$a_3 = 3^3 + 3 = 27 + 3 = 30$
The sequence is 2, 10, 30, ...
The difference between consecutive terms is $a_2 - a_1 = 10 - 2 = 8$ and $a_3 - a_2 = 30 - 10 = 20$.
Since the difference between consecutive terms is not constant ($8 \neq 20$), this sequence is not an AP. Thus, $n^3 + n$ cannot be the $n^{th}$ term of an AP.
Based on the analysis, only the expression that is a linear function of $n$ can be the $n^{th}$ term of an AP.
Therefore, only $3n + 1$ can be the $n^{th}$ term of an AP.
Question 12. Are the points (–3, –3), (–3, 2) and (–3, 5) collinear? Give reasons.
Answer:
Given:
The three points are A(–3, –3), B(–3, 2), and C(–3, 5).
To Determine:
If the points are collinear.
Solution:
Points are said to be collinear if they lie on the same straight line.
We can check for collinearity by examining the coordinates of the given points.
Let the coordinates of the points be $A(x_1, y_1)$, $B(x_2, y_2)$, and $C(x_3, y_3)$.
Here, $x_1 = -3$, $y_1 = -3$
$x_2 = -3$, $y_2 = 2$
$x_3 = -3$, $y_3 = 5$
Observe the x-coordinates of the three points:
The x-coordinate of A is –3.
The x-coordinate of B is –3.
The x-coordinate of C is –3.
All three points have the same x-coordinate, which is –3.
If multiple points have the same x-coordinate and different y-coordinates, they lie on a vertical line defined by that x-coordinate. In this case, all three points lie on the line $x = -3$.
Since all three points lie on the same vertical line, they are collinear.
Reason:
The points (–3, –3), (–3, 2), and (–3, 5) are collinear because they all lie on the vertical line with the equation $x = -3$. Any set of points with the same x-coordinate lies on a vertical line.
Alternatively (using Slope):
We can also check for collinearity by calculating the slopes between pairs of points.
Slope of line segment AB = $\frac{y_2 - y_1}{x_2 - x_1} = \frac{2 - (-3)}{-3 - (-3)} = \frac{2 + 3}{-3 + 3} = \frac{5}{0}$. The slope is undefined.
Slope of line segment BC = $\frac{y_3 - y_2}{x_3 - x_2} = \frac{5 - 2}{-3 - (-3)} = \frac{3}{-3 + 3} = \frac{3}{0}$. The slope is undefined.
Since the slopes of AB and BC are both undefined and they share a common point B, the points A, B, and C lie on the same vertical line.
Conclusion:
Yes, the points (–3, –3), (–3, 2), and (–3, 5) are collinear.
Question 13. ABC and BDE are two equilateral triangles such that D is the mid point of BC. What is the ratio of the areas of triangles ABC and BDE? Justify your answer.
Answer:
Given:
$\triangle ABC$ and $\triangle BDE$ are equilateral triangles.
D is the midpoint of BC.
To Find:
The ratio of the areas of triangles ABC and BDE, Area$(\triangle ABC)$ : Area$(\triangle BDE)$.
Solution:
Since both $\triangle ABC$ and $\triangle BDE$ are equilateral triangles, all their angles are equal to $60^\circ$.
Triangles with equal corresponding angles are similar. Therefore, $\triangle ABC \sim \triangle BDE$.
According to the theorem on the ratio of areas of similar triangles, the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle BDE)} = \left(\frac{\text{Side of } \triangle ABC}{\text{Corresponding side of } \triangle BDE}\right)^2$
Let the side length of equilateral triangle ABC be $s$. So, $AB = BC = AC = s$.
Given that D is the midpoint of BC.
BD = $\frac{1}{2} BC$
(D is the midpoint of BC)
Since $BC = s$, we have $BD = \frac{1}{2} s$.
$\triangle BDE$ is an equilateral triangle. Since B is a vertex and D is on BC, and D is the midpoint of BC, the side length of $\triangle BDE$ must be BD.
Side length of $\triangle BDE = BD = \frac{1}{2}s$. Thus, $BD = DE = EB = \frac{1}{2}s$.
The corresponding sides of similar triangles $\triangle ABC$ and $\triangle BDE$ can be taken as BC and BD.
The ratio of corresponding sides is $\frac{BC}{BD} = \frac{s}{s/2} = \frac{s}{s} \$ \times \$ 2 = 2$.
Now, we find the ratio of their areas using the property of similar triangles:
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle BDE)} = \left(\frac{BC}{BD}\right)^2$
$\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle BDE)} = (2)^2 = 4$
The ratio of the areas of triangles ABC and BDE is $4:1$.
Justification:
1. Similarity: All equilateral triangles have angles of $60^\circ$, making them similar to each other. Hence, $\triangle ABC \sim \triangle BDE$.
2. Area Ratio Property: For similar triangles, the ratio of their areas is the square of the ratio of their corresponding sides. $\frac{\text{Area}(\triangle ABC)}{\text{Area}(\triangle BDE)} = \left(\frac{\text{Side}_1}{\text{Side}_2}\right)^2$, where Side$_1$ and Side$_2$ are corresponding sides.
3. Side Length Relationship: Given that D is the midpoint of BC and $\triangle BDE$ is an equilateral triangle built on BD, the side length of $\triangle BDE$ (BD) is half the side length of $\triangle ABC$ (BC).
BD = $\frac{1}{2} BC$
(From given information)
4. Ratio Calculation: The ratio of the corresponding sides BC to BD is $\frac{BC}{BD} = \frac{BC}{\frac{1}{2} BC} = 2$.
5. Final Ratio: Squaring the ratio of sides, $\left(\frac{BC}{BD}\right)^2 = (2)^2 = 4$. Thus, the ratio of the areas is 4.
The ratio of the areas of triangles ABC and BDE is $4:1$.
Question 14. cos (A + B) = $\frac{1}{2}$ and sin (A - B) = $\frac{1}{2}$, 0° < A + B < 90° and A – B > 0°. What are the values of ∠A and ∠B? Justify your answer.
Answer:
Given:
The equations $\cos (A + B) = \frac{1}{2}$ and $\sin (A - B) = \frac{1}{2}$.
The conditions $0^\circ < A + B < 90^\circ$ and $A – B > 0^\circ$.
To Find:
The values of angles ∠A and ∠B.
Solution and Justification:
We are given that $\cos (A + B) = \frac{1}{2}$.
We know that $\cos 60^\circ = \frac{1}{2}$.
Since $0^\circ < A + B < 90^\circ$, the angle $(A + B)$ must be in the first quadrant. In the first quadrant, the cosine function is positive, and the only angle whose cosine is $\frac{1}{2}$ is $60^\circ$.
$A + B = 60^\circ$
[From $\cos(A+B) = 1/2$] ... (i)
We are also given that $\sin (A - B) = \frac{1}{2}$.
We know that $\sin 30^\circ = \frac{1}{2}$.
The condition $A - B > 0^\circ$ means the angle $(A - B)$ is positive. Since $A+B < 90^\circ$ and $A-B > 0$, A and B must be positive, and $A > B$. This implies that $A-B$ is an angle smaller than $A+B$. Considering the values of A and B that might result from the first equation, $A-B$ is also likely in the first quadrant. In the first quadrant, the only angle whose sine is $\frac{1}{2}$ is $30^\circ$.
A - B = $30^\circ$
[From $\sin(A-B) = 1/2$] ... (ii)
Now we have a system of two linear equations with two variables, A and B:
A + B = $60^\circ$
... (i)
A - B = $30^\circ$
... (ii)
To find A, we can add Equation (i) and Equation (ii):
(A + B) + (A - B) = $60^\circ$ + $30^\circ$
2A = $90^\circ$
A = $\frac{90^\circ}{2}$
A = $45^\circ$
To find B, substitute the value of A into Equation (i):
$45^\circ$ + B = $60^\circ$
B = $60^\circ$ - $45^\circ$
B = $15^\circ$
Verification:
Let's check if these values satisfy the given conditions:
$A + B = 45^\circ + 15^\circ = 60^\circ$. The condition $0^\circ < 60^\circ < 90^\circ$ is satisfied.
$A - B = 45^\circ - 15^\circ = 30^\circ$. The condition $30^\circ > 0^\circ$ is satisfied.
Also, $\cos(60^\circ) = \frac{1}{2}$ and $\sin(30^\circ) = \frac{1}{2}$, which match the given equations.
The values of ∠A and ∠B are uniquely determined by the given equations and constraints.
The value of ∠A is $45^\circ$ and the value of ∠B is $15^\circ$.
Question 15. A coin is tossed twice and the outcome is noted every time. Can you say that head must come once in two tosses? Justify your answer.
OR
A die is thrown once. The probability of getting a prime number is $\frac{2}{3}$. Is it true? Justify your answer.
Answer:
Solution for the first part (Coin Toss):
Given Statement: A coin is tossed twice. Can you say that head must come once?
Justification:
When a coin is tossed twice, the possible outcomes are listed below. The sample space is the set of all possible outcomes.
Let H represent getting a Head and T represent getting a Tail.
The possible outcomes are:
1. First toss is Head, second toss is Head (HH)
2. First toss is Head, second toss is Tail (HT)
3. First toss is Tail, second toss is Head (TH)
4. First toss is Tail, second toss is Tail (TT)
The sample space $S = \{HH, HT, TH, TT\}$. The total number of outcomes is 4.
The statement "head must come once in two tosses" implies that it is certain that at least one head will occur in any sequence of two tosses.
Let's examine the outcomes:
- In HH, a head comes twice (which satisfies "at least once").
- In HT, a head comes once.
- In TH, a head comes once.
- In TT, a head does not come at all (zero heads).
Since there is an outcome (TT) where no head appears, it is not guaranteed that a head must come once in two tosses.
Therefore, the statement is false.
Conclusion for the first part: No, it is not true that head must come once in two tosses.
Solution for the second part (Die Roll):
Given Statement: A die is thrown once. The probability of getting a prime number is $\frac{2}{3}$. Is it true?
Justification:
When a standard six-sided die is thrown once, the possible outcomes are the integers from 1 to 6.
The sample space is $S = \{1, 2, 3, 4, 5, 6\}$.
The total number of possible outcomes is $|S| = 6$.
We need to identify the prime numbers in the sample space $S$. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
- 1 is not prime.
- 2 is prime (divisors are 1 and 2).
- 3 is prime (divisors are 1 and 3).
- 4 is not prime (divisors are 1, 2, and 4).
- 5 is prime (divisors are 1 and 5).
- 6 is not prime (divisors are 1, 2, 3, and 6).
The prime numbers in the sample space are $\{2, 3, 5\}$.
Let $E$ be the event of getting a prime number. The set of favorable outcomes is $E = \{2, 3, 5\}$.
The number of favorable outcomes is $|E| = 3$.
The probability of an event E is calculated as:
$P(E) = \frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes}}$
$P(\text{getting a prime number}) = \frac{|E|}{|S|} = \frac{3}{6}$
Simplify the fraction:
$P(\text{getting a prime number}) = \frac{\cancel{3}^1}{\cancel{6}_2} = \frac{1}{2}$
The calculated probability of getting a prime number when throwing a die once is $\frac{1}{2}$.
The given statement says the probability is $\frac{2}{3}$.
Since $\frac{1}{2} \neq \frac{2}{3}$, the statement is false.
Conclusion for the second part: No, the statement is not true.
Section C
Question 16. Show that square of an odd positive integer is of the form 8q + 1, for some positive integer q.
OR
Write the denominator of the rational number $\frac{357}{5000}$ in the form of 2m 5n , m, n are non-negative integers and hence write its decimal expansion, without actual division.
Answer:
Solution for the OR part:
Given:
The rational number is $\frac{357}{5000}$.
To Find:
1. The denominator of the rational number in the form $2^m 5^n$, where $m, n$ are non-negative integers.
2. The decimal expansion of the rational number without actual division.
Solution:
The denominator of the given rational number $\frac{357}{5000}$ is 5000.
We need to find the prime factorization of the denominator 5000.
$\begin{array}{c|cc} 2 & 5000 \\ \hline 2 & 2500 \\ \hline 2 & 1250 \\ \hline 5 & 625 \\ \hline 5 & 125 \\ \hline 5 & 25 \\ \hline 5 & 5 \\ \hline & 1 \end{array}$
So, the prime factorization of 5000 is $2 \times 2 \times 2 \times 5 \times 5 \times 5 \times 5 = 2^3 \times 5^4$.
We can write the denominator in the form $2^m 5^n$ as $2^3 \times 5^4$.
Here, $m = 3$ and $n = 4$. Both 3 and 4 are non-negative integers.
To write the decimal expansion without actual division, we need to convert the denominator into a power of 10. A power of 10 can be written as $10^k = (2 \times 5)^k = 2^k \times 5^k$.
Our denominator is $2^3 \times 5^4$. To make the powers of 2 and 5 equal, we need to match the higher power, which is 4.
We need $2^4 \times 5^4$. Currently, we have $2^3 \times 5^4$. We need one more factor of 2 ($2^{4-3} = 2^1$).
Multiply the numerator and the denominator by 2:
$\frac{357}{5000} = \frac{357}{2^3 \times 5^4} = \frac{357 \times 2}{2^3 \times 5^4 \times 2^1}$
$\frac{357 \times 2}{2^4 \times 5^4} = \frac{714}{(2 \times 5)^4} = \frac{714}{10^4} = \frac{714}{10000}$
To write $\frac{714}{10000}$ as a decimal, we move the decimal point 4 places to the left from the end of the numerator (714), since the denominator is $10^4$ (which has 4 zeroes).
Starting from 714.0, move the decimal point 4 places left: 714.0 $\to$ 71.40 $\to$ 7.140 $\to$ 0.7140 $\to$ 0.0714.
The decimal expansion is 0.0714.
Summary:
The denominator is $5000 = 2^3 \times 5^4$, where $m=3$ and $n=4$, which are non-negative integers.
The decimal expansion of $\frac{357}{5000}$ is 0.0714.
Question 17. If (x – 2) is a factor of x3 + ax2 + bx + 16 and b = 4a, then find the values of a and b.
Answer:
Given:
The polynomial $P(x) = x^3 + ax^2 + bx + 16$.
$(x - 2)$ is a factor of $P(x)$.
The relationship between $a$ and $b$ is $b = 4a$.
To Find:
The values of $a$ and $b$.
Solution:
According to the Factor Theorem, if $(x - c)$ is a factor of a polynomial $P(x)$, then $P(c) = 0$.
In this case, $(x - 2)$ is a factor of $P(x)$, so $P(2)$ must be equal to 0.
Substitute $x = 2$ into the polynomial $P(x) = x^3 + ax^2 + bx + 16$:
$P(2) = (2)^3 + a(2)^2 + b(2) + 16$
$P(2) = 8 + 4a + 2b + 16$
$P(2) = 4a + 2b + 24$
Since $(x - 2)$ is a factor, $P(2) = 0$.
4a + 2b + 24 = 0
... (i)
We are also given the relationship $b = 4a$.
b = 4a
... (ii)
Now we have a system of two linear equations with two variables $a$ and $b$. We can solve this system by substituting Equation (ii) into Equation (i).
Substitute $b = 4a$ into Equation (i):
$4a + 2(4a) + 24 = 0$}
$4a + 8a + 24 = 0$}
$12a + 24 = 0$}
Solve for $a$:
$12a = -24$}
$a = \frac{-24}{12}$}
$a = -2$}
Now substitute the value of $a = -2$ into Equation (ii) to find the value of $b$:
$b = 4a$}
$b = 4(-2)$}
$b = -8$}
Thus, the values are $a = -2$ and $b = -8$.
Verification:
Check if $b = 4a$: $-8 = 4(-2)$, which is $-8 = -8$. This is true.
Check if $(x-2)$ is a factor of $x^3 - 2x^2 - 8x + 16$. We need to check if $P(2) = 0$ with $a=-2$ and $b=-8$.
$P(2) = (2)^3 + (-2)(2)^2 + (-8)(2) + 16$}
$P(2) = 8 - 2(4) - 16 + 16$}
$P(2) = 8 - 8 - 16 + 16$}
$P(2) = 0$}
Since $P(2) = 0$, $(x - 2)$ is indeed a factor.
The values are $a = -2$ and $b = -8$.
Question 18. The sum of reciprocals of a child’s age (in years) 3 years ago and 5 years from now $\frac{1}{3}$. Find his present age.
OR
Solve for x : 6 a2x2 – 7abx – 3b2 = 0, a ≠ 0, using the quadratic formula.
Answer:
Solution for the first part:
Given:
The sum of the reciprocals of a child's age 3 years ago and 5 years from now is $\frac{1}{3}$.
To Find:
The child's present age.
Solution:
Let the present age of the child be $x$ years.
The child's age 3 years ago was $x - 3$ years.
The child's age 5 years from now will be $x + 5$ years.
The reciprocal of the age 3 years ago is $\frac{1}{x - 3}$.
The reciprocal of the age 5 years from now is $\frac{1}{x + 5}$.
According to the problem, the sum of these reciprocals is $\frac{1}{3}$.
$\frac{1}{x - 3} + \frac{1}{x + 5} = \frac{1}{3}$
... (i)
To solve this equation, find a common denominator for the left side, which is $(x - 3)(x + 5)$.
$\frac{(x + 5) + (x - 3)}{(x - 3)(x + 5)} = \frac{1}{3}$
Simplify the numerator:
$\frac{x + 5 + x - 3}{x^2 + 5x - 3x - 15} = \frac{1}{3}$
$\frac{2x + 2}{x^2 + 2x - 15} = \frac{1}{3}$
Cross-multiply:
$3(2x + 2) = 1(x^2 + 2x - 15)$
$6x + 6 = x^2 + 2x - 15$
Rearrange the terms to form a quadratic equation by moving all terms to one side:
$x^2 + 2x - 15 - 6x - 6 = 0$
$x^2 + (2x - 6x) + (-15 - 6) = 0$}
$x^2 - 4x - 21 = 0$}
We can solve this quadratic equation by factoring, completing the square, or using the quadratic formula.
Let's try factoring. We need two numbers that multiply to -21 and add up to -4. These numbers are -7 and 3.
So, we can factor the quadratic expression as $(x - 7)(x + 3) = 0$.
Setting each factor to zero to find the possible values of $x$:
$x - 7 = 0 \implies x = 7$}
$x + 3 = 0 \implies x = -3$}
Since age cannot be negative, the solution $x = -3$ is rejected.
The present age of the child must be a positive value.
So, the present age of the child is $x = 7$ years.
Verification:
Age 3 years ago = $7 - 3 = 4$ years. Reciprocal = $\frac{1}{4}$.
Age 5 years from now = $7 + 5 = 12$ years. Reciprocal = $\frac{1}{12}$.
Sum of reciprocals = $\frac{1}{4} + \frac{1}{12} = \frac{3}{12} + \frac{1}{12} = \frac{3 + 1}{12} = \frac{4}{12} = \frac{1}{3}$.
The sum matches the given condition. Also, the age must be such that $x-3 \neq 0$ and $x+5 \neq 0$, which means $x \neq 3$ and $x \neq -5$. Our solution $x=7$ satisfies these conditions.
The present age of the child is 7 years.
Solution for the OR part:
Given:
The quadratic equation $6 a^2x^2 – 7abx – 3b^2 = 0$, where $a \neq 0$.
To Find:
The values of $x$ using the quadratic formula.
Solution:
The given equation is in the standard form of a quadratic equation $Ax^2 + Bx + C = 0$, where the variable is $x$.
Comparing the given equation $6a^2x^2 – 7abx – 3b^2 = 0$ with the standard form, we have:
$A = 6a^2$
$B = -7ab$
$C = -3b^2$
The quadratic formula for the roots of $Ax^2 + Bx + C = 0$ is:
$x = \frac{-B \pm \sqrt{B^2 - 4AC}}{2A}$
Calculate the discriminant, $D = B^2 - 4AC$:
$D = (-7ab)^2 - 4(6a^2)(-3b^2)$
$D = 49a^2b^2 - 4(-18a^2b^2)$
$D = 49a^2b^2 + 72a^2b^2$
$D = 121a^2b^2$
Now, find the square root of the discriminant:
$\sqrt{D} = \sqrt{121a^2b^2} = \sqrt{121} \times \sqrt{a^2} \times \sqrt{b^2} = 11 \times |a| \times |b|$.
Assuming $a$ and $b$ are real numbers, we can write $\sqrt{121a^2b^2} = \pm 11ab$ (since $a^2b^2 = (ab)^2$, $\sqrt{(ab)^2} = |ab|$, and the $\pm$ sign in the quadratic formula already accounts for the positive and negative roots).
Substitute the values of A, B, and $\sqrt{D}$ into the quadratic formula:
$x = \frac{-(-7ab) \pm \sqrt{121a^2b^2}}{2(6a^2)}$
$x = \frac{7ab \pm 11ab}{12a^2}$
Find the two possible values for $x$:
Case 1: Using the + sign
$x_1 = \frac{7ab + 11ab}{12a^2} = \frac{18ab}{12a^2}$
Simplify the expression by cancelling common factors (assuming $a \neq 0$):
$x_1 = \frac{\cancel{18}^{3} \cancel{a} b}{\cancel{12}_{2} a^{\cancel{2}}} = \frac{3b}{2a}$
Case 2: Using the – sign
$x_2 = \frac{7ab - 11ab}{12a^2} = \frac{-4ab}{12a^2}$
Simplify the expression by cancelling common factors (assuming $a \neq 0$):
$x_2 = \frac{-\cancel{4}^{1} \cancel{a} b}{\cancel{12}_{3} a^{\cancel{2}}} = \frac{-b}{3a}$
The solutions for $x$ are $\frac{3b}{2a}$ and $\frac{-b}{3a}$.
The values of x are $\frac{3b}{2a}$ and $\frac{-b}{3a}$.
Question 19. Find the sum of all two digit natural numbers which are divisible by 7.
Answer:
Given:
We need to find the sum of all two-digit natural numbers that are divisible by 7.
To Find:
The sum of the specified numbers.
Solution:
The two-digit natural numbers are integers from 10 to 99.
We need to identify the two-digit numbers that are divisible by 7.
The first two-digit number divisible by 7 is $7 \times 2 = 14$.
The next numbers are $14 + 7 = 21$, $21 + 7 = 28$, and so on.
These numbers form an Arithmetic Progression (AP) with the first term $a = 14$ and the common difference $d = 7$.
Now, we need to find the last two-digit number divisible by 7.
The largest two-digit number is 99. Let's divide 99 by 7:
$99 \div 7$. $99 = 7 \times 14 + 1$.
This means 99 leaves a remainder of 1 when divided by 7. To find the largest multiple of 7 less than or equal to 99, we subtract the remainder from 99: $99 - 1 = 98$.
So, the last two-digit number divisible by 7 is 98. This is the last term of the AP, $l = 98$.
The AP is 14, 21, 28, ..., 98.
We need to find the number of terms ($n$) in this AP.
Using the formula for the $n^{th}$ term of an AP, $a_n = a + (n-1)d$, where $a_n = l = 98$, $a = 14$, and $d = 7$.
98 = 14 + (n - 1)7
... (i)
Subtract 14 from both sides:
$98 - 14 = (n - 1)7$
$84 = (n - 1)7$
Divide both sides by 7:
$\frac{84}{7} = n - 1$
$12 = n - 1$
Add 1 to both sides:
$n = 12 + 1$
$n = 13$
There are 13 two-digit natural numbers divisible by 7.
Now we need to find the sum of these 13 terms. The sum of an AP ($S_n$) can be calculated using the formula $S_n = \frac{n}{2}(a + l)$.
Here, $n = 13$, $a = 14$, and $l = 98$.
$S_{13} = \frac{13}{2}(14 + 98)$
$S_{13} = \frac{13}{2}(112)$
Divide 112 by 2:
$S_{13} = 13 \times 56$
Perform the multiplication:
$\begin{array}{cc}& & 5 & 6 \\ \times & & 1 & 3 \\ \hline & 1 & 6 & 8 \\ 5 & 6 & \times \\ \hline 7 & 2 & 8 \\ \hline \end{array}$
$S_{13} = 728$
The sum of all two-digit natural numbers divisible by 7 is 728.
The sum is 728.
Question 20. Find the ratio in which the line x + 3y – 14 = 0 divides the line segment joining the points A (–2, 4) and B (3, 7).
Answer:
Given:
The line is given by the equation $L: x + 3y - 14 = 0$.
The line segment joins points $A(-2, 4)$ and $B(3, 7)$.
To Find:
The ratio in which the line $L$ divides the line segment AB.
Solution:
Let the line $x + 3y - 14 = 0$ divide the line segment joining $A(-2, 4)$ and $B(3, 7)$ in the ratio $k : 1$ at a point $P(x, y)$.
Using the section formula, the coordinates of point P are:
$x = \frac{k x_2 + 1 x_1}{k + 1} = \frac{k(3) + 1(-2)}{k + 1} = \frac{3k - 2}{k + 1}$
$y = \frac{k y_2 + 1 y_1}{k + 1} = \frac{k(7) + 1(4)}{k + 1} = \frac{7k + 4}{k + 1}$
Since the point $P(x, y)$ lies on the line $x + 3y - 14 = 0$, its coordinates must satisfy the equation of the line.
Substitute the expressions for $x$ and $y$ into the equation of the line:
$\left(\frac{3k - 2}{k + 1}\right) + 3\left(\frac{7k + 4}{k + 1}\right) - 14 = 0$
Multiply the entire equation by $(k + 1)$ to eliminate the denominators (assuming $k + 1 \neq 0$, which is true since $k$ is a ratio and $k \neq -1$ for a division):
$(3k - 2) + 3(7k + 4) - 14(k + 1) = 0$
Distribute the terms:
$3k - 2 + 21k + 12 - 14k - 14 = 0$
Combine like terms (terms with $k$ and constant terms):
$(3k + 21k - 14k) + (-2 + 12 - 14) = 0$
$(24k - 14k) + (10 - 14) = 0$
$10k - 4 = 0$
Solve for $k$:
$10k = 4$
$k = \frac{4}{10}$
Simplify the fraction:
$k = \frac{\cancel{4}^2}{\cancel{10}_5} = \frac{2}{5}$
The ratio is $k : 1$, which is $\frac{2}{5} : 1$.
To express this as a simple ratio, multiply both parts by 5:
$\left(\frac{2}{5} \times 5\right) : (1 \times 5) = 2 : 5$
Since $k$ is positive, the division is internal. The line divides the segment AB internally in the ratio 2:5.
Alternate Method (Ratio Formula for Line Division):
The ratio in which a line $Ax + By + C = 0$ divides the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is given by the formula:
Ratio $= -\frac{Ax_1 + By_1 + C}{Ax_2 + By_2 + C}$
For the line $x + 3y - 14 = 0$, we have $A = 1$, $B = 3$, $C = -14$.
For point $A(-2, 4)$, we have $x_1 = -2$, $y_1 = 4$.
For point $B(3, 7)$, we have $x_2 = 3$, $y_2 = 7$.
Substitute these values into the formula:
Ratio $= -\frac{(1)(-2) + (3)(4) + (-14)}{(1)(3) + (3)(7) + (-14)}$
Ratio $= -\frac{-2 + 12 - 14}{3 + 21 - 14}$
Ratio $= -\frac{10 - 14}{24 - 14}$
Ratio $= -\frac{-4}{10}$
Ratio $= \frac{4}{10}$
Ratio $= \frac{2}{5}$
The ratio is $\frac{2}{5}$, which means the ratio is $2 : 5$. Since the ratio is positive, the division is internal.
The line divides the line segment joining the points A and B in the ratio 2:5.
Question 21. Find the area of the quadrilateral whose vertices in the same order are (–4, –2), (–3, –5), (3, –2) and (2, 3).
Answer:
Given:
The vertices of the quadrilateral are A(–4, –2), B(–3, –5), C(3, –2), and D(2, 3), taken in order.
To Find:
The area of the quadrilateral ABCD.
Solution:
We can find the area of the quadrilateral by dividing it into two triangles using a diagonal. Let's use the diagonal AC to divide the quadrilateral ABCD into two triangles: $\triangle ABC$ and $\triangle ADC$.
The formula for the area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Area of $\triangle ABC$:
The vertices are A(–4, –2), B(–3, –5), and C(3, –2).
$(x_1, y_1) = (-4, -2)$
$(x_2, y_2) = (-3, -5)$
$(x_3, y_3) = (3, -2)$
Area($\triangle ABC$) $= \frac{1}{2} |(-4)(-5 - (-2)) + (-3)(-2 - (-2)) + (3)(-2 - (-5))|$
Area($\triangle ABC$) $= \frac{1}{2} |(-4)(-5 + 2) + (-3)(-2 + 2) + (3)(-2 + 5)|$}
Area($\triangle ABC$) $= \frac{1}{2} |(-4)(-3) + (-3)(0) + (3)(3)|$}
Area($\triangle ABC$) $= \frac{1}{2} |12 + 0 + 9|$}
Area($\triangle ABC$) $= \frac{1}{2} |21| = \frac{21}{2}$ square units.
Area of $\triangle ADC$:
The vertices are A(–4, –2), D(2, 3), and C(3, –2).
Let's take them in the order A $\to$ C $\to$ D for calculation ease with diagonal AC.
Vertices A(–4, –2), C(3, –2), D(2, 3).
$(x_1, y_1) = (-4, -2)$
$(x_2, y_2) = (3, -2)$
$(x_3, y_3) = (2, 3)$
Area($\triangle ACD$) $= \frac{1}{2} |(-4)(-2 - 3) + (3)(3 - (-2)) + (2)(-2 - (-2))|$
Area($\triangle ACD$) $= \frac{1}{2} |(-4)(-5) + (3)(3 + 2) + (2)(-2 + 2)|$}
Area($\triangle ACD$) $= \frac{1}{2} |20 + (3)(5) + (2)(0)|$}
Area($\triangle ACD$) $= \frac{1}{2} |20 + 15 + 0|$}
Area($\triangle ACD$) $= \frac{1}{2} |35| = \frac{35}{2}$ square units.
Area of Quadrilateral ABCD:
The area of the quadrilateral ABCD is the sum of the areas of $\triangle ABC$ and $\triangle ACD$.
Area(ABCD) = Area($\triangle ABC$) + Area($\triangle ACD$)
Area(ABCD) $= \frac{21}{2} + \frac{35}{2}$
Area(ABCD) $= \frac{21 + 35}{2}$}
Area(ABCD) $= \frac{56}{2}$}
Area(ABCD) $= 28$ square units.
The area of the quadrilateral is 28 square units.
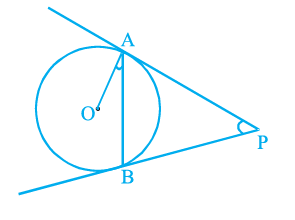
Question 22. Two tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that ∠APB = 2∠OAB. (see the following figure).
Answer:
Given:
A circle with centre O.
Two tangents PA and PB are drawn from an external point P to the circle.
To Prove:
$\angle APB = 2\angle OAB$.
Proof:
In $\triangle OAP$ and $\triangle OBP$:
OA = OB
(Radii of the same circle)
OP = OP
(Common side)
PA = PB
(Tangents from an external point to a circle are equal in length)
Therefore, $\triangle OAP \cong \triangle OBP$ by SSS congruence criterion.
By CPCT (Corresponding Parts of Congruent Triangles), we have:
$\angle APO = \angle BPO$
$\angle AOP = \angle BOP$
Let $\angle APB = 2\theta$. Then $\angle APO = \angle BPO = \theta$.
Consider the triangle $\triangle OAP$. The angle between the radius and the tangent at the point of contact is $90^\circ$.
$\angle OAP = 90^\circ$
(Radius is perpendicular to the tangent at the point of contact)
In right-angled triangle $\triangle OAP$, the sum of angles is $180^\circ$.
$\angle OAP + \angle APO + \angle AOP = 180^\circ$
$90^\circ + \theta + \angle AOP = 180^\circ$
$\angle AOP = 180^\circ - 90^\circ - \theta = 90^\circ - \theta$
We have $\angle AOB = \angle AOP + \angle BOP$. Since $\angle AOP = \angle BOP$, we have $\angle AOB = 2 \angle AOP$.
$\angle AOB = 2 (90^\circ - \theta) = 180^\circ - 2\theta$.
Now, consider $\triangle OAB$. OA = OB (radii), so $\triangle OAB$ is an isosceles triangle. The angles opposite to equal sides are equal.
$\angle OAB = \angle OBA$
(Angles opposite to equal sides OA and OB)
In $\triangle OAB$, the sum of angles is $180^\circ$.
$\angle OAB + \angle OBA + \angle AOB = 180^\circ$
$\angle OAB + \angle OAB + (180^\circ - 2\theta) = 180^\circ$
$2\angle OAB + 180^\circ - 2\theta = 180^\circ$
$2\angle OAB = 180^\circ - 180^\circ + 2\theta$
$2\angle OAB = 2\theta$
$\angle OAB = \theta$
We defined $\angle APB = 2\theta$. Substituting $\theta = \angle OAB$, we get:
$\angle APB = 2 \angle OAB$
Justification:
1. PA = PB because tangents from an external point to a circle are equal.
2. $\triangle OAP \cong \triangle OBP$ by SSS criterion, which leads to $\angle APO = \angle BPO$ and $\angle AOP = \angle BOP$.
3. The angle between a radius and a tangent at the point of contact is $90^\circ$, so $\angle OAP = 90^\circ$.
4. In $\triangle OAP$, $\angle AOP = 90^\circ - \angle APO$.
5. In $\triangle OAB$, OA = OB (radii), so it is isosceles, and $\angle OAB = \angle OBA$.
6. Sum of angles in $\triangle OAB$ is $180^\circ$, so $2\angle OAB + \angle AOB = 180^\circ$.
7. $\angle AOB = 2\angle AOP = 2(90^\circ - \angle APO) = 180^\circ - 2\angle APO$.
8. Substituting $\angle AOB$ in the sum of angles of $\triangle OAB$: $2\angle OAB + 180^\circ - 2\angle APO = 180^\circ$, which simplifies to $2\angle OAB = 2\angle APO$, or $\angle OAB = \angle APO$.
9. Since $\angle APB = 2\angle APO$ (from $\angle APO = \angle BPO$), substituting $\angle APO = \angle OAB$, we get $\angle APB = 2\angle OAB$.
Hence Proved.
Question 23. Construct a triangle with sides 3 cm, 5 cm and 7 cm and then construct another triangle whose sides are $\frac{5}{3}$ of the corresponding sides of the first triangle.
Answer:
Construction:
We are asked to construct a triangle with given side lengths and then a similar triangle with a given scale factor.
Step 1: Construction of the first triangle (with sides 3 cm, 5 cm, and 7 cm)
Let the first triangle be $\triangle ABC$ with sides $AB = 3$ cm, $AC = 5$ cm, and $BC = 7$ cm.
(i) Draw a line segment BC of length 7 cm.
(ii) With B as the centre, draw an arc with a radius equal to 3 cm.
(iii) With C as the centre, draw an arc with a radius equal to 5 cm.
(iv) Let the two arcs intersect at point A.
(v) Join AB and AC.
Thus, $\triangle ABC$ is the required triangle with side lengths 3 cm, 5 cm, and 7 cm.
Step 2: Construction of the similar triangle (with sides $\frac{5}{3}$ of the corresponding sides of $\triangle ABC$)
We need to construct a triangle similar to $\triangle ABC$ with sides $\frac{5}{3}$ times the corresponding sides of $\triangle ABC$. The scale factor is $\frac{5}{3}$. Since the scale factor is greater than 1, the new triangle will be larger than $\triangle ABC$.
Let the new triangle be $\triangle A'BC'$.
(i) Draw a ray BX starting from B, making an acute angle with BC. This ray should be drawn on the opposite side of vertex A.
(ii) Mark 5 points, $B_1, B_2, B_3, B_4, B_5$, on the ray BX such that $BB_1 = B_1B_2 = B_2B_3 = B_3B_4 = B_4B_5$. (Since the numerator of the scale factor is 5, we mark 5 points).
(iii) Join $B_3$ (the point corresponding to the denominator 3) to C.
(iv) Draw a line through $B_5$ parallel to $B_3C$. To do this, place the compass at $B_3$ and draw an arc intersecting $BB_5$ and $B_3C$. With the same compass setting, place the compass at $B_5$ and draw a similar arc intersecting $BB_5$. Measure the distance between the intersection points of the first arc with $B_3C$ and $BB_5$. Transfer this distance to the second arc starting from the intersection point on $BB_5$. The point where the transferred arc intersects the second arc gives the direction for the parallel line. Draw the line passing through $B_5$ and this intersection point.
(v) Extend the line segment BC. The line through $B_5$ parallel to $B_3C$ will intersect the extended line segment BC at a point. Let this point be C'.
(vi) Draw a line through C' parallel to the side AC. To do this, draw an arc from C intersecting BC and AC. With the same radius, draw an arc from C' intersecting the extended line BC'. Measure the distance between the intersection points of the first arc. Transfer this distance to the second arc from the intersection point on the extended BC'. The point where the transferred arc intersects the second arc gives the direction for the parallel line. Draw the line passing through C' and this intersection point.
(vii) Extend the line segment BA. The line through C' parallel to AC will intersect the extended line segment BA at a point. Let this point be A'.
Thus, $\triangle A'BC'$ is the required triangle whose sides are $\frac{5}{3}$ times the corresponding sides of $\triangle ABC$.
Justification:
By construction, the line $B_5C'$ is parallel to $B_3C$. By the Basic Proportionality Theorem (Thales's Theorem) in $\triangle BB_5C'$, since $B_3C \parallel B_5C'$, we have:
$\frac{BC}{CC'} = \frac{BB_3}{B_3B_5}$
From our construction, $BB_3 = 3$ units and $B_3B_5 = BB_5 - BB_3 = 5 - 3 = 2$ units.
So, $\frac{BC}{CC'} = \frac{3}{2}$.
This means $CC' = \frac{2}{3} BC$.
Then $BC' = BC + CC' = BC + \frac{2}{3} BC = \frac{3+2}{3} BC = \frac{5}{3} BC$.
Also, by construction, $A'C'$ is parallel to AC. Since $A'C' \parallel AC$, $\triangle A'BC'$ is similar to $\triangle ABC$ by AA similarity criterion (or AAA, as the angles will be the same).
Since $\triangle A'BC' \sim \triangle ABC$, the ratio of corresponding sides is equal:
$\frac{A'B}{AB} = \frac{A'C'}{AC} = \frac{BC'}{BC}$
We found $BC' = \frac{5}{3} BC$, so $\frac{BC'}{BC} = \frac{5}{3}$.
Therefore, $\frac{A'B}{AB} = \frac{A'C'}{AC} = \frac{BC'}{BC} = \frac{5}{3}$.
This shows that the sides of $\triangle A'BC'$ are $\frac{5}{3}$ times the corresponding sides of $\triangle ABC$.
Question 24. Prove the identity (1 + cot θ + tan θ) (sin θ – cos θ) = $\frac{\sec\theta}{cosecc^2 \;\theta} -\frac{cosec\;\theta}{\sec^2\theta}$
OR
Find the value of $\frac{cos^{2}\;32^\circ \;+\; cos^{2}\;58^\circ}{sec^{2}\;50^\circ \;-\; sec^{2}\;40^\circ}$ - 4 tan 13° tan 37° tan 53° tan 77°
Answer:
Solution for the OR part (Evaluation):
Let the given expression be E.
E $= \frac{\cos^{2}\;32^\circ \;+\; \cos^{2}\;58^\circ}{\sec^{2}\;50^\circ \;-\; \sec^{2}\;40^\circ}$ - 4 tan 13° tan 37° tan 53° tan 77°
Consider the first term: $\frac{\cos^{2}\;32^\circ \;+\; \cos^{2}\;58^\circ}{\sec^{2}\;50^\circ \;-\; \sec^{2}\;40^\circ}$.
Using $\cos(90^\circ - \theta) = \sin \theta$, the numerator is $\cos^2 32^\circ + \cos^2 (90^\circ - 32^\circ) = \cos^2 32^\circ + \sin^2 32^\circ = 1$.
Using $\sec(90^\circ - \theta) = \text{cosec } \theta$, the denominator is $\sec^2 50^\circ - \sec^2 (90^\circ - 50^\circ) = \sec^2 50^\circ - \text{cosec}^2 50^\circ$.
Assuming a common typo, the denominator was likely intended to be $\sec^{2}\;50^\circ \;-\; \cot^{2}\;40^\circ$. Using $\cot 40^\circ = \tan (90^\circ - 40^\circ) = \tan 50^\circ$, this becomes $\sec^2 50^\circ - \tan^2 50^\circ = 1$.
Under this assumption, the first term is $\frac{1}{1} = 1$.
Consider the second term: $- 4 \tan 13^\circ \tan 37^\circ \tan 53^\circ \tan 77^\circ$.
Group terms using complementary angles: $(13^\circ + 77^\circ = 90^\circ)$ and $(37^\circ + 53^\circ = 90^\circ)$.
$\tan 77^\circ = \tan (90^\circ - 13^\circ) = \cot 13^\circ$.
$\tan 53^\circ = \tan (90^\circ - 37^\circ) = \cot 37^\circ$.
The second term $= - 4 (\tan 13^\circ \cot 13^\circ) (\tan 37^\circ \cot 37^\circ)$.
Using $\tan \theta \cot \theta = 1$, this becomes $- 4 (1) (1) = -4$.
Combining the results (assuming the typo in the first term):
E $= 1 + (-4) = 1 - 4 = -3$.
The value of the expression is -3.
Question 25. The area of an equilateral triangle is 49$\sqrt{3}$ cm2. Taking each vertex as centre, circles are described with radius equal to half the length of the side of the triangle. Find the area of the part of the triangle not included in the circles. [Take $\sqrt{3}$ = 1.73, $\pi=\frac{22}{7}$
Answer:
Given:
Area of the equilateral triangle = $49\sqrt{3}$ cm$^2$.
Circles are drawn with each vertex as the centre.
Radius of each circle = half the length of the side of the triangle.
$\sqrt{3} = 1.73$
$\pi = \frac{22}{7}$
To Find:
Area of the part of the triangle not included in the circles.
Solution:
Let the side length of the equilateral triangle be $a$ cm.
The area of an equilateral triangle with side $a$ is given by the formula: Area $= \frac{\sqrt{3}}{4} a^2$.
We are given the area is $49\sqrt{3}$ cm$^2$.
$49\sqrt{3} = \frac{\sqrt{3}}{4} a^2$
... (i)
Divide both sides by $\sqrt{3}$:
$49 = \frac{1}{4} a^2$
Multiply both sides by 4:
$a^2 = 49 \times 4 = 196$
Taking the square root:
$a = \sqrt{196} = 14$ cm
The side length of the equilateral triangle is 14 cm.
The radius of each circle is half the length of the side of the triangle.
Radius, $r = \frac{1}{2} a = \frac{1}{2} \times 14 = 7$ cm.
At each vertex of the equilateral triangle, the angle is $60^\circ$. The portion of each circle inside the triangle is a sector with a central angle of $60^\circ$ and radius $r = 7$ cm.
The area of one such sector is given by: Area of sector $= \frac{\theta}{360^\circ} \times \pi r^2$.
Area of one sector $= \frac{60^\circ}{360^\circ} \times \pi (7)^2 = \frac{1}{6} \times \pi \times 49$ cm$^2$.
Since there are three such sectors (one at each vertex) within the triangle, the total area of these three sectors is $3 \times (\text{Area of one sector})$.
Total area of sectors $= 3 \times \frac{1}{6} \times \pi \times 49 = \frac{1}{2} \times \pi \times 49$ cm$^2$.
Using the given value $\pi = \frac{22}{7}$:
Total area of sectors $= \frac{1}{2} \times \frac{22}{7} \times 49$
Total area of sectors $= \frac{1}{2} \times 22 \times \frac{\cancel{49}^7}{\cancel{7}_1} = \frac{1}{2} \times 22 \times 7 = 11 \times 7 = 77$ cm$^2$.
The area of the part of the triangle not included in the circles is the area of the triangle minus the total area of the three sectors within the triangle.
Required Area = Area of $\triangle$ - Total area of sectors
Required Area $= 49\sqrt{3} - 77$ cm$^2$.
Using the given value $\sqrt{3} = 1.73$:
Required Area $= 49 \times 1.73 - 77$
Calculate $49 \times 1.73$:
$49 \times 1.73 = 84.77$
Required Area $= 84.77 - 77$
Required Area $= 7.77$ cm$^2$.
The area of the part of the triangle not included in the circles is 7.77 cm$^2$.
Section D
Question 26. In a bag containing white and red balls, half the number of white balls is equal to the one third the number of red balls. Twice the total number of balls exceeds three times the number of red balls by 8. How many balls of each type does the bag contain?
Answer:
Given:
A bag contains white and red balls.
Condition 1: Half the number of white balls is equal to one third the number of red balls.
Condition 2: Twice the total number of balls exceeds three times the number of red balls by 8.
To Find:
The number of white balls and the number of red balls.
Solution:
Let the number of white balls be $w$.
Let the number of red balls be $r$.
From Condition 1, "half the number of white balls is equal to one third the number of red balls":
$\frac{1}{2} w = \frac{1}{3} r$
... (i)
Multiply both sides by 6 to clear the denominators:
$6 \times \frac{1}{2} w = 6 \times \frac{1}{3} r$
$3w = 2r$
We can express $w$ in terms of $r$: $w = \frac{2}{3}r$.
The total number of balls is $w + r$.
From Condition 2, "Twice the total number of balls exceeds three times the number of red balls by 8":
2 (w + r) = 3r + 8
... (ii)
Expand the left side of the equation:
$2w + 2r = 3r + 8$
Now we have a system of two linear equations with two variables $w$ and $r$:
3w = 2r
... (i)
2w + 2r = 3r + 8
... (ii)
From equation (i), $w = \frac{2}{3}r$. Substitute this expression for $w$ into equation (ii).
$2\left(\frac{2}{3}r\right) + 2r = 3r + 8$}
$\frac{4}{3}r + 2r = 3r + 8$}
Combine the terms with $r$ on the left side. Find a common denominator (3):
$\frac{4}{3}r + \frac{6}{3}r = 3r + 8$}
$\frac{4r + 6r}{3} = 3r + 8$}
$\frac{10r}{3} = 3r + 8$}
Multiply both sides by 3 to eliminate the denominator:
$3 \times \frac{10r}{3} = 3 \times (3r + 8)$}
$10r = 9r + 24$}
Subtract 9r from both sides:
$10r - 9r = 24$}
$r = 24$}
The number of red balls is 24.
Now, substitute the value of $r = 24$ into equation (i) to find the value of $w$:
$3w = 2r$}
$3w = 2(24)$}
$3w = 48$}
Divide both sides by 3:
$w = \frac{48}{3}$}
$w = 16$}
The number of white balls is 16.
Verification:
Check Condition 1: Half the number of white balls = $\frac{1}{2} \times 16 = 8$. One third the number of red balls = $\frac{1}{3} \times 24 = 8$. This condition is satisfied.
Check Condition 2: Total number of balls = $w + r = 16 + 24 = 40$.
Twice the total number of balls = $2 \times 40 = 80$.
Three times the number of red balls = $3 \times 24 = 72$.
Does twice the total number of balls exceed three times the number of red balls by 8? $80 - 72 = 8$. Yes, this condition is satisfied.
The bag contains 16 white balls and 24 red balls.
Question 27. Prove that in a right triangle, the square of the hypotenuse is equal to sum of squares of the other two sides.
Using the above theorem, prove that in a triangle ABC, if AD is perpendicular to BC, then AB2 + CD2 = AC2 + BD2.
Answer:
Part 1: Proof of Pythagorean Theorem
Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Given:
A right triangle ABC, right-angled at C.
To Prove:
$AB^2 = AC^2 + BC^2$.
Construction:
Draw a perpendicular CD from vertex C to the hypotenuse AB. Let D be a point on AB.
Proof:
In $\triangle ADC$ and $\triangle ACB$:
$\angle ADC = \angle ACB = 90^\circ$
(By construction and Given)
$\angle CAD = \angle CAB$
(Common angle)
Therefore, $\triangle ADC \sim \triangle ACB$ by AA similarity criterion.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{AD}{AC} = \frac{AC}{AB} = \frac{CD}{CB}$
From the first two ratios, we get:
$\frac{AD}{AC} = \frac{AC}{AB}$
$AC^2 = AD \times AB$
$AC^2 = AD \times AB$
... (1)
In $\triangle BDC$ and $\triangle BCA$:
$\angle BDC = \angle BCA = 90^\circ$
(By construction and Given)
$\angle CBD = \angle CBA$
(Common angle)
Therefore, $\triangle BDC \sim \triangle BCA$ by AA similarity criterion.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{BD}{BC} = \frac{BC}{BA} = \frac{DC}{AC}$
From the first two ratios, we get:
$\frac{BD}{BC} = \frac{BC}{BA}$
$BC^2 = BD \times BA$
$BC^2 = BD \times AB$
... (2)
Add equation (1) and equation (2):
$AC^2 + BC^2 = (AD \times AB) + (BD \times AB)$
$AC^2 + BC^2 = AB (AD + BD)$
From the figure, D lies on AB, so $AD + BD = AB$.
$AC^2 + BC^2 = AB (AB)$
(Since $AD + BD = AB$)
$AC^2 + BC^2 = AB^2$
Thus, the square of the hypotenuse (AB) is equal to the sum of the squares of the other two sides (AC and BC).
Hence Proved (Pythagorean Theorem).
Part 2: Using the Theorem to Prove the Identity
Given:
Triangle ABC.
AD is perpendicular to BC, where D is a point on BC.
To Prove:
$AB^2 + CD^2 = AC^2 + BD^2$.
Proof:
Since AD is perpendicular to BC, we have two right-angled triangles formed: $\triangle ADB$ and $\triangle ADC$. Both triangles are right-angled at D.
Apply the Pythagorean theorem to $\triangle ADB$:
In $\triangle ADB$, $AB^2 = AD^2 + BD^2$
... (3)
(By Pythagorean theorem in right $\triangle ADB$)
Apply the Pythagorean theorem to $\triangle ADC$:
In $\triangle ADC$, $AC^2 = AD^2 + CD^2$
... (4)
(By Pythagorean theorem in right $\triangle ADC$)
From equation (4), we can express $AD^2$ as:
AD$^2$ = $AC^2 - CD^2$
... (5)
Substitute the expression for $AD^2$ from equation (5) into equation (3):
$AB^2 = (AC^2 - CD^2) + BD^2$
$AB^2 = AC^2 - CD^2 + BD^2$
Rearrange the terms by adding $CD^2$ to both sides of the equation:
$AB^2 + CD^2 = AC^2 + BD^2$
Thus, we have proved that in a triangle ABC, if AD is perpendicular to BC, then $AB^2 + CD^2 = AC^2 + BD^2$.
Hence Proved.
Question 28. A pole 5m high is fixed on the top of a tower. The angle of elevation of the top of the pole as observed from a point A on the ground is 60° and the angle of depression of point A from the top of the tower is 45°. Find the height of the tower. (Take $\sqrt{3}$ = 1.73)
Answer:
Given:
Height of the pole fixed on top of a tower = 5 m.
Angle of elevation of the top of the pole from point A on the ground = $60^\circ$.
Angle of depression of point A from the top of the tower = $45^\circ$.
$\sqrt{3} = 1.73$.
To Find:
The height of the tower.
Solution:
Let BC represent the tower with height $h$ meters (where B is the base on the ground and C is the top of the tower).
Let CD represent the pole on top of the tower, so CD = 5 m.
The total height from the ground to the top of the pole is BD = BC + CD = $h + 5$ meters.
Let A be the point on the ground from which the observations are made. Let AB be the horizontal distance from the base of the tower to point A. Let AB = $x$ meters.
The angle of depression of point A from the top of the tower (C) is $45^\circ$. If we draw a horizontal line through C, the angle between this line and CA is $45^\circ$. Since the horizontal line through C is parallel to the ground AB, the angle of elevation of C from A, $\angle CAB$, is equal to the angle of depression, $45^\circ$ (alternate interior angles).
In the right-angled triangle $\triangle ABC$ (right-angled at B):
$\tan(\angle CAB) = \frac{BC}{AB}$
$\tan 45^\circ = \frac{h}{x}$
Since $\tan 45^\circ = 1$:
$1 = \frac{h}{x}$
h = x
... (i)
The angle of elevation of the top of the pole (D) from point A on the ground is $60^\circ$.
In the right-angled triangle $\triangle ABD$ (right-angled at B):
$\tan(\angle DAB) = \frac{BD}{AB}$
$\tan 60^\circ = \frac{h+5}{x}$
Since $\tan 60^\circ = \sqrt{3}$:
$\sqrt{3} = \frac{h+5}{x}$
... (ii)
Substitute $x = h$ from Equation (i) into Equation (ii):
$\sqrt{3} = \frac{h+5}{h}$
Multiply both sides by $h$:
$h\sqrt{3} = h + 5$
Rearrange the terms to isolate $h$:
$h\sqrt{3} - h = 5$
Factor out $h$:
$h(\sqrt{3} - 1) = 5$}
Divide by $(\sqrt{3} - 1)$:
$h = \frac{5}{\sqrt{3} - 1}$}
To rationalize the denominator, multiply the numerator and denominator by the conjugate of the denominator, which is $(\sqrt{3} + 1)$:
$h = \frac{5}{(\sqrt{3} - 1)} \times \frac{(\sqrt{3} + 1)}{(\sqrt{3} + 1)}$
$h = \frac{5(\sqrt{3} + 1)}{(\sqrt{3})^2 - 1^2}$
$h = \frac{5(\sqrt{3} + 1)}{3 - 1}$
$h = \frac{5(\sqrt{3} + 1)}{2}$}
Substitute the given value $\sqrt{3} = 1.73$:
$h = \frac{5(1.73 + 1)}{2}$}
$h = \frac{5(2.73)}{2}$}
Calculate $5 \times 2.73$:
$5 \times 2.73 = 13.65$
$h = \frac{13.65}{2}$}
Calculate the final value of $h$:
$h = 6.825$}
The height of the tower is 6.825 meters.
The height of the tower is 6.825 m.
Question 29. The interior of a building is in the form of a cylinder of diameter 4 m and height 3.5 m, surmounted by a cone of the same base with vertical angle as a right angle. Find the surface area (curved) and volume of the interior of the building.
OR
A vessel in the form of an open inverted cone of height 8 cm and radius of its top is 5 cm. It is filled with water up to the brim. When lead shots, each of radius 0.5 cm are dropped into the vessel, one fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Answer:
Solution for the first part (Building with Cylinder and Cone):
Given:
Building shape: Cylinder surmounted by a cone.
Cylinder: Diameter = 4 m, Height ($h_c$) = 3.5 m.
Cone: Same base as cylinder, Vertical angle is a right angle ($90^\circ$).
To Find:
The curved surface area and the volume of the interior of the building.
Solution:
Radius of the cylinder, $r = \frac{\text{Diameter}}{2} = \frac{4}{2} = 2$ m.
Since the cone has the same base as the cylinder, the radius of the cone is also $r = 2$ m.
For the cone, the vertical angle is $90^\circ$. The vertical angle is the angle at the vertex of the cone. If we draw a cross-section through the axis of the cone, we get an isosceles triangle where the angle at the vertex is $90^\circ$. This triangle is formed by the height ($h_k$) and slant height ($l$) of the cone, and the radius ($r$). The two slant heights are equal, and the base is the diameter of the base of the cone (2r).
Let the vertical angle be $\alpha = 90^\circ$. The semi-vertical angle is $\frac{\alpha}{2} = \frac{90^\circ}{2} = 45^\circ$.
In the right triangle formed by the height ($h_k$), radius ($r$), and slant height ($l$) of the cone, we have $\tan(\text{semi-vertical angle}) = \frac{\text{radius}}{\text{height}}$.
$\tan 45^\circ = \frac{r}{h_k}$
Since $\tan 45^\circ = 1$ and $r = 2$ m:
$1 = \frac{2}{h_k}$
$h_k = 2$ m
The height of the cone is 2 m.
Now, calculate the slant height $l$ of the cone using the Pythagorean theorem:
$l^2 = r^2 + h_k^2$
$l^2 = (2)^2 + (2)^2 = 4 + 4 = 8$
$l = \sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2}$ m.
Curved Surface Area of the interior of the building:
This consists of the curved surface area of the cylinder and the curved surface area of the cone.
Curved Surface Area of cylinder $= 2 \pi r h_c$
Curved Surface Area of cone $= \pi r l$
Total Curved Surface Area = Curved Surface Area of cylinder + Curved Surface Area of cone
Total CSA $= 2 \pi (2) (3.5) + \pi (2) (2\sqrt{2})$
Total CSA $= 14\pi + 4\sqrt{2}\pi = (14 + 4\sqrt{2})\pi$ m$^2$.
Using $\pi = \frac{22}{7}$ and $\sqrt{2} \approx 1.414$ (not given in the problem, but often used if $\sqrt{3}$ is given; let's keep it in terms of $\pi$ and $\sqrt{2}$ unless a decimal value is required or implied by options):
Total CSA $= (14 + 4\sqrt{2})\pi$ m$^2$.
If we need a numerical value and use $\pi=\frac{22}{7}$ and the problem only provides $\sqrt{3}=1.73$, there might be an expectation to leave $\sqrt{2}$ as is or use an approximate value. Let's keep it in terms of $\pi$ and $\sqrt{2}$.
Volume of the interior of the building:
This consists of the volume of the cylinder and the volume of the cone.
Volume of cylinder $= \pi r^2 h_c$
Volume of cone $= \frac{1}{3} \pi r^2 h_k$
Total Volume = Volume of cylinder + Volume of cone
Total Volume $= \pi (2)^2 (3.5) + \frac{1}{3} \pi (2)^2 (2)$
Total Volume $= \pi (4) (3.5) + \frac{1}{3} \pi (4) (2)$
Total Volume $= 14\pi + \frac{8}{3}\pi$
Find a common denominator:
Total Volume $= \frac{14 \times 3}{3}\pi + \frac{8}{3}\pi = \frac{42\pi + 8\pi}{3} = \frac{50\pi}{3}$ m$^3$.
Using $\pi = \frac{22}{7}$:
Total Volume $= \frac{50}{3} \times \frac{22}{7} = \frac{50 \times 22}{3 \times 7} = \frac{1100}{21}$ m$^3$.
$\frac{1100}{21} \approx 52.38$ m$^3$.
So, the curved surface area is $(14 + 4\sqrt{2})\pi$ m$^2$ and the volume is $\frac{1100}{21}$ m$^3$.
Let's provide the curved surface area with $\pi=\frac{22}{7}$ as well, although $\sqrt{2}$ is not given. If a numerical answer is expected, using $\sqrt{2} \approx 1.414$ is reasonable.
Total CSA $= (14 + 4 \times 1.414) \times \frac{22}{7}$
$= (14 + 5.656) \times \frac{22}{7} = 19.656 \times \frac{22}{7}$
$= \frac{432.432}{7} \approx 61.776$ m$^2$. This seems less likely without a $\sqrt{2}$ value.
Let's keep the CSA in terms of $\pi$ and $\sqrt{2}$.
Curved Surface Area $= (14\pi + 4\sqrt{2}\pi)$ m$^2$
Volume $= \frac{1100}{21}$ m$^3$
The curved surface area of the interior of the building is $(14\pi + 4\sqrt{2}\pi)$ m$^2$ and the volume is $\frac{1100}{21}$ m$^3$.
Solution for the OR part (Cone and Lead Shots):
Given:
Vessel is an open inverted cone.
Height of the cone ($H$) = 8 cm.
Radius of the top of the cone ($R$) = 5 cm.
The cone is filled with water up to the brim.
Lead shots are dropped into the vessel, each a sphere with radius ($r$) = 0.5 cm.
One fourth of the water flows out when lead shots are dropped.
To Find:
The number of lead shots dropped in the vessel.
Solution:
The volume of water that flows out is equal to the total volume of the lead shots dropped in the vessel (assuming the shots are fully submerged and the water level was at the brim initially).
Volume of the cone (vessel) $= \frac{1}{3} \pi R^2 H$
Volume of the cone $= \frac{1}{3} \pi (5)^2 (8) = \frac{1}{3} \pi (25)(8) = \frac{200\pi}{3}$ cm$^3$.
This is the initial volume of water in the vessel.
Volume of water that flows out = $\frac{1}{4}$ of the Volume of the cone
Volume of water flowed out $= \frac{1}{4} \times \frac{200\pi}{3} = \frac{50\pi}{3}$ cm$^3$.
Each lead shot is a sphere with radius $r = 0.5$ cm.
Volume of one lead shot (sphere) $= \frac{4}{3} \pi r^3$
Volume of one lead shot $= \frac{4}{3} \pi (0.5)^3 = \frac{4}{3} \pi \left(\frac{1}{2}\right)^3 = \frac{4}{3} \pi \left(\frac{1}{8}\right) = \frac{\pi}{6}$ cm$^3$.
Let $n$ be the number of lead shots dropped in the vessel.
The total volume of $n$ lead shots is $n \times (\text{Volume of one lead shot}) = n \times \frac{\pi}{6}$.
The total volume of the lead shots is equal to the volume of water that flows out.
$n \times \frac{\pi}{6} = \frac{50\pi}{3}$
We need to solve for $n$. We can cancel $\pi$ from both sides (since $\pi \neq 0$).
$n \times \frac{1}{6} = \frac{50}{3}$
Multiply both sides by 6:
$n = \frac{50}{3} \times 6 = 50 \times \frac{\cancel{6}^2}{\cancel{3}_1} = 50 \times 2 = 100$.
The number of lead shots dropped in the vessel is 100.
The number of lead shots dropped in the vessel is 100.
Question 30. Find the mean, median and mode of the following frequency distribution:
| Class | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 |
|---|---|---|---|---|---|---|---|
| Frequency | 4 | 5 | 7 | 10 | 12 | 18 | 4 |
OR
The following distribution gives the daily income of 50 workers of a factory:
| Daily income (in Rs) | 100 - 120 | 120 - 140 | 140 - 160 | 160 - 180 | 180 - 200 |
|---|---|---|---|---|---|
| Number if workers | 12 | 14 | 8 | 6 | 10 |
Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive. Find the median from this ogive.
Answer:
Solution for the first part (Mean, Median, Mode):
Given:
Frequency distribution table:
| Class | Frequency ($f_i$) |
| 0 - 10 | 4 |
| 10 - 20 | 5 |
| 20 - 30 | 7 |
| 30 - 40 | 10 |
| 40 - 50 | 12 |
| 50 - 60 | 18 |
| 60 - 70 | 4 |
To Find:
Mean, Median, and Mode of the distribution.
Calculations for Mean:
We will use the direct method to find the mean. We need to find the class mark ($x_i$) for each class and the product $f_i x_i$.
Class Mark ($x_i$) = $\frac{\text{Lower Limit} + \text{Upper Limit}}{2}$.
| Class | Frequency ($f_i$) | Class Mark ($x_i$) | $f_i x_i$ |
| 0 - 10 | 4 | $\frac{0+10}{2} = 5$ | $4 \times 5 = 20$ |
| 10 - 20 | 5 | $\frac{10+20}{2} = 15$ | $5 \times 15 = 75$ |
| 20 - 30 | 7 | $\frac{20+30}{2} = 25$ | $7 \times 25 = 175$ |
| 30 - 40 | 10 | $\frac{30+40}{2} = 35$ | $10 \times 35 = 350$ |
| 40 - 50 | 12 | $\frac{40+50}{2} = 45$ | $12 \times 45 = 540$ |
| 50 - 60 | 18 | $\frac{50+60}{2} = 55$ | $18 \times 55 = 990$ |
| 60 - 70 | 4 | $\frac{60+70}{2} = 65$ | $4 \times 65 = 260$ |
| Total | $\sum f_i = 60$ | $\sum f_i x_i = 2410$ |
Total frequency, $N = \sum f_i = 4 + 5 + 7 + 10 + 12 + 18 + 4 = 60$.
Sum of $f_i x_i$, $\sum f_i x_i = 20 + 75 + 175 + 350 + 540 + 990 + 260 = 2410$.
Mean $(\bar{x}) = \frac{\sum f_i x_i}{\sum f_i} = \frac{2410}{60}$.
$\bar{x} = \frac{241}{6} = 40.166...$
Mean $\approx 40.17$.
Calculations for Median:
We need to find the cumulative frequencies (cf).
| Class | Frequency ($f_i$) | Cumulative Frequency (cf) |
| 0 - 10 | 4 | 4 |
| 10 - 20 | 5 | 4 + 5 = 9 |
| 20 - 30 | 7 | 9 + 7 = 16 |
| 30 - 40 | 10 | 16 + 10 = 26 |
| 40 - 50 | 12 | 26 + 12 = 38 |
| 50 - 60 | 18 | 38 + 18 = 56 |
| 60 - 70 | 4 | 56 + 4 = 60 |
Total frequency, $N = 60$.
The median class is the class where the cumulative frequency is greater than or equal to $\frac{N}{2}$.
$\frac{N}{2} = \frac{60}{2} = 30$.
The cumulative frequency just greater than 30 is 38, which corresponds to the class 40 - 50. So, the median class is 40 - 50.
For the median class 40 - 50:
Lower limit of median class, $l = 40$.
Cumulative frequency of the class preceding the median class, $cf = 26$.
Frequency of the median class, $f = 12$.
Class size, $h = 10$ (e.g., 10 - 0 = 10).
Median $= l + \left(\frac{\frac{N}{2} - cf}{f}\right) \times h$
Median $= 40 + \left(\frac{30 - 26}{12}\right) \times 10$
Median $= 40 + \left(\frac{4}{12}\right) \times 10$
Median $= 40 + \left(\frac{1}{3}\right) \times 10 = 40 + \frac{10}{3}$
Median $= 40 + 3.333... = 43.333...$
Median $\approx 43.33$.
Calculations for Mode:
The modal class is the class with the highest frequency.
From the frequency table, the highest frequency is 18, which corresponds to the class 50 - 60.
So, the modal class is 50 - 60.
For the modal class 50 - 60:
Lower limit of modal class, $l = 50$.
Frequency of the modal class, $f_1 = 18$.
Frequency of the class preceding the modal class, $f_0 = 12$ (frequency of 40-50).
Frequency of the class succeeding the modal class, $f_2 = 4$ (frequency of 60-70).
Class size, $h = 10$.
Mode $= l + \left(\frac{f_1 - f_0}{2f_1 - f_0 - f_2}\right) \times h$
Mode $= 50 + \left(\frac{18 - 12}{2(18) - 12 - 4}\right) \times 10$
Mode $= 50 + \left(\frac{6}{36 - 12 - 4}\right) \times 10$
Mode $= 50 + \left(\frac{6}{36 - 16}\right) \times 10$
Mode $= 50 + \left(\frac{6}{20}\right) \times 10$
Mode $= 50 + \frac{6}{2} = 50 + 3 = 53$.
Summary:
Mean $\approx 40.17$
Median $\approx 43.33$
Mode $= 53$
The mean is approximately 40.17, the median is approximately 43.33, and the mode is 53.
Solution for the OR part (Cumulative Frequency and Ogive):
Given:
Frequency distribution of daily income:
| Daily income (in ₹) | Number of workers ($f_i$) |
| 100 - 120 | 12 |
| 120 - 140 | 14 |
| 140 - 160 | 8 |
| 160 - 180 | 6 |
| 180 - 200 | 10 |
Total number of workers = 50.
To Find:
1. Convert the distribution to a less than type cumulative frequency distribution.
2. Draw its ogive.
3. Find the median from this ogive.
Less Than Type Cumulative Frequency Distribution:
We need to find the number of workers with daily income less than the upper limit of each class interval.
| Daily income | Cumulative Frequency (cf) |
| Less than 120 | 12 |
| Less than 140 | 12 + 14 = 26 |
| Less than 160 | 26 + 8 = 34 |
| Less than 180 | 34 + 6 = 40 |
| Less than 200 | 40 + 10 = 50 |
To draw the less than ogive, we plot the upper limits of the class intervals on the x-axis and the corresponding cumulative frequencies on the y-axis.
The points to be plotted are (120, 12), (140, 26), (160, 34), (180, 40), (200, 50).
We also start the ogive from a point on the x-axis corresponding to the lower limit of the first class with a cumulative frequency of 0. In this case, the lower limit is 100, so the starting point is (100, 0).
Plot the points (100, 0), (120, 12), (140, 26), (160, 34), (180, 40), (200, 50) on a graph paper and join them with a free hand curve. This curve is the less than ogive.
Finding Median from the Ogive:
The median is the value on the x-axis corresponding to a cumulative frequency of $\frac{N}{2}$.
Total number of workers, $N = 50$.
$\frac{N}{2} = \frac{50}{2} = 25$.
To find the median from the ogive:
(i) Locate the point on the y-axis corresponding to a cumulative frequency of 25.
(ii) From this point, draw a horizontal line parallel to the x-axis to intersect the ogive.
(iii) From the point of intersection on the ogive, draw a vertical line parallel to the y-axis to intersect the x-axis.
(iv) The point where the vertical line intersects the x-axis is the median.
Looking at the cumulative frequency table, the cf value 25 lies between 12 and 26. This is within the class 120 - 140.
On the ogive, find the x-value where the y-value is 25. This value will be between 120 and 140.
By observing a precisely drawn ogive, the x-value corresponding to y=25 should be approximately 138.57.
Calculation of Median using Formula (for verification):
Median class is 120 - 140 (since cf=26 is the first cf $\geq$ 25).
$l = 120$
$cf = 12$ (cf of preceding class)
$f = 14$ (frequency of median class)
$h = 20$ (class size)
Median $= l + \left(\frac{\frac{N}{2} - cf}{f}\right) \times h = 120 + \left(\frac{25 - 12}{14}\right) \times 20$
Median $= 120 + \left(\frac{13}{14}\right) \times 20 = 120 + \frac{260}{14} = 120 + \frac{130}{7}$
Median $= 120 + 18.5714... \approx 138.57$
The median found from the ogive should be approximately equal to the calculated median.
The median from the ogive is approximately 138.57 ₹.

